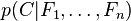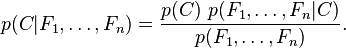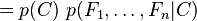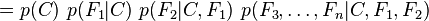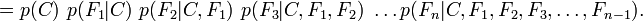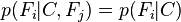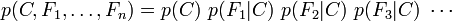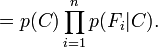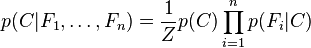Machine learning naive_bayes_classifier (finished).

http://en.wikipedia.org/wiki/Naive_Bayes_classifier

 

 

Abstractly, the probability model for a classifier is a conditional model 模型：

 可以展开为

In plain English the above equation can be written as

 

关键是计算分子，因为分母为常数

而分子可以展开为

The numerator is equivalent to the joint probability model

which can be rewritten as follows, using repeated applications of the definition of conditional probability:

Now the "naive" conditional independence assumptions come into play: assume that each feature F_i is conditionally independent of every other feature F_j for 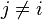. This means that

for , and so the joint model can be expressed as

This means that under the above independence assumptions, the conditional distribution over the class variable C can be expressed like this:这里是最终的分子：

 

Constructing a classifier from the probability model

The discussion so far has derived the independent feature model, that is, the naive Bayes probability model. The naive Bayes classifier combines this model with a decision rule. One common rule is to pick the hypothesis that is most probable; this is known as the maximum a posteriori or MAP decision rule. The corresponding classifier is the function classify defined as follows:贝叶斯分类器的构造，通常为使用最大似然优化以下函数

更详细的判别函数，及参数估计（最大似然及贝叶斯参数估计）的推导最好看书， 推荐《模式分类》

 

• 上一篇 Implementing semaphores, locks and condition variables.
• 下一篇 Machine learning others in opencv.